Výsledky a řešení jarního matematického testu 2017

 

Podívejte se na klíč správných odpovědí všech maturitních příkladů z ostrého jarního didaktického testu z matematiky 2017. Zkontrolujte si, jak jste u maturitního testu 2017 zabodovali a zda jste došli ke správným matematickým výsledkům. Řešené postupy všech maturitních úloh z podzimu maturity 2017 poslouží i studentům připravujícím se na maturitní termíny v následujících letech maturitních ročníků. Šiřte vzorová vypracování a sdílejte je se svými přáteli a spolužáky k užitku všech. Dobrá znalost matematiky se vám neztratí u maturity, ani v životě.

maturita-matika-prijimacky-vs-medicina-bmedic

Vyřešené zadání pro didaktický test z matematiky - jaro 2017

Zadání didaktického testu z matematiky 2017 jaro

Zadání úlohy 1

Řešení úlohy 1

Zadání úlohy 2

Řešení úlohy 2

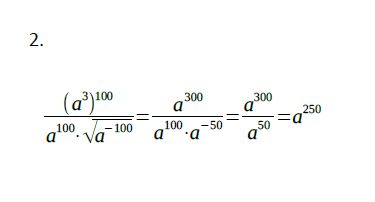
Zadání úlohy 3

Řešení úlohy 3

Zadání úlohy 4

Řešení úlohy 4

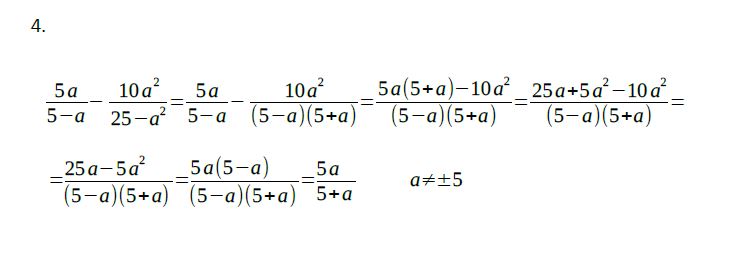
Zadání úlohy 5

Řešení úlohy 5

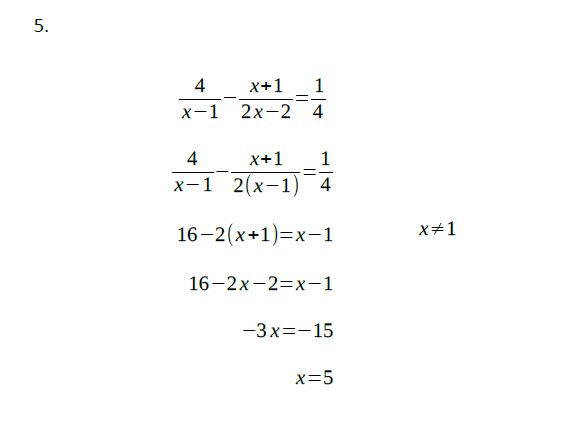
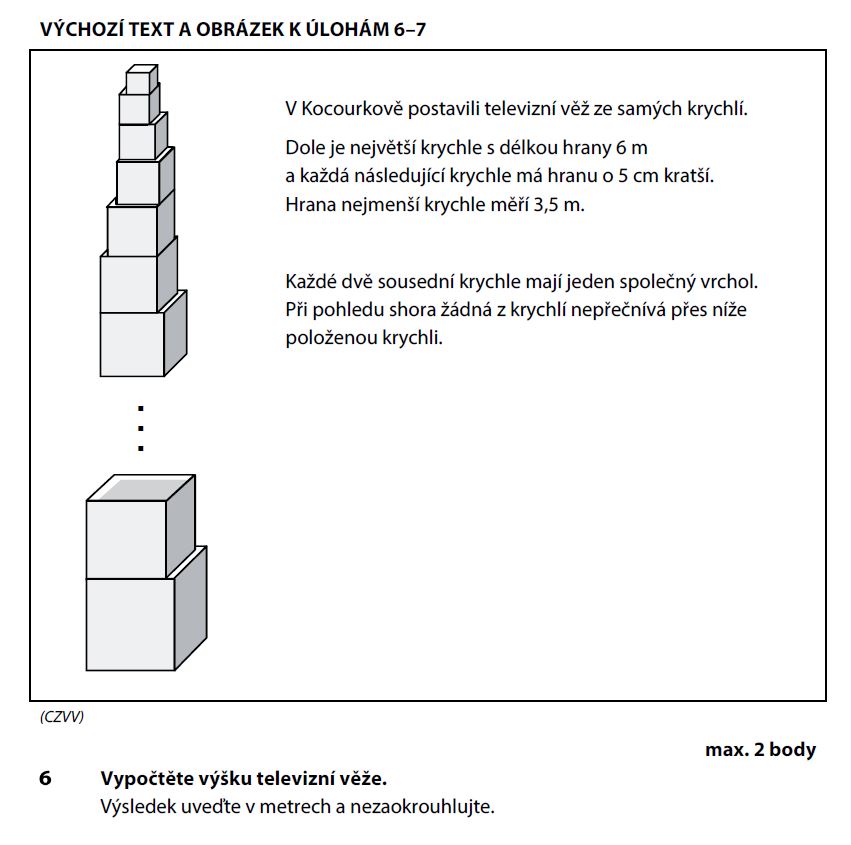
Zadání úlohy 6

Řešení úlohy 6

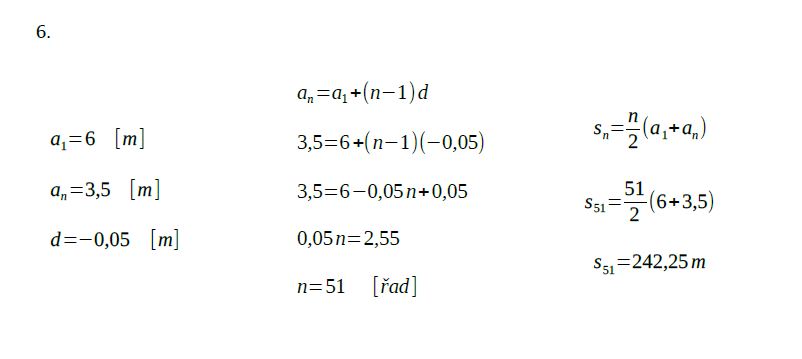
Zadání úlohy 7

Řešení úlohy 7

Zadání úlohy 8

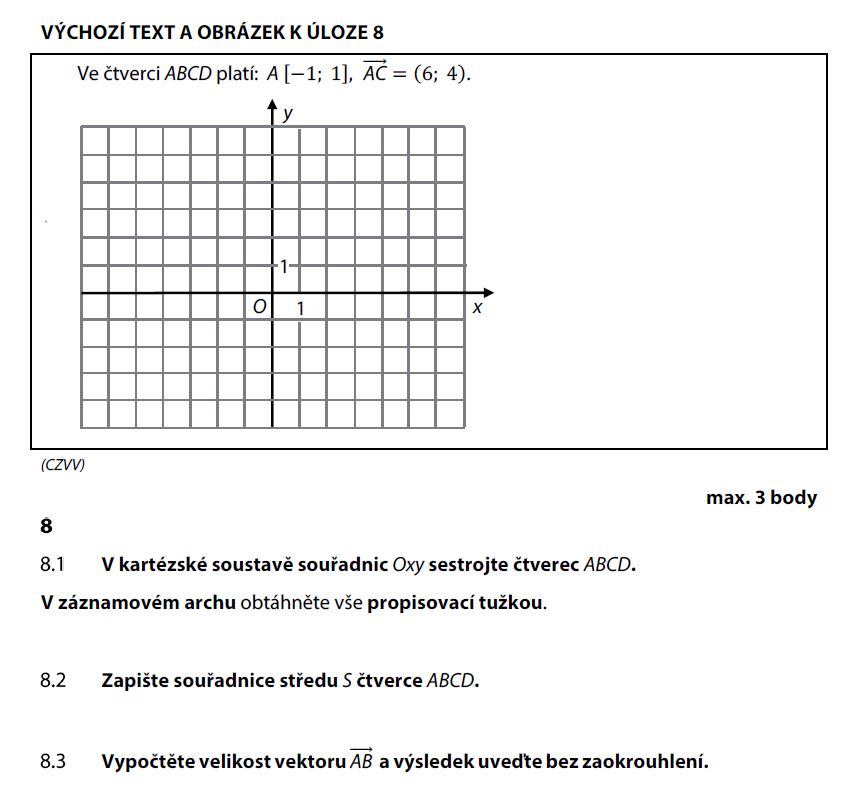
Řešení úlohy 8

Zadání úlohy 9

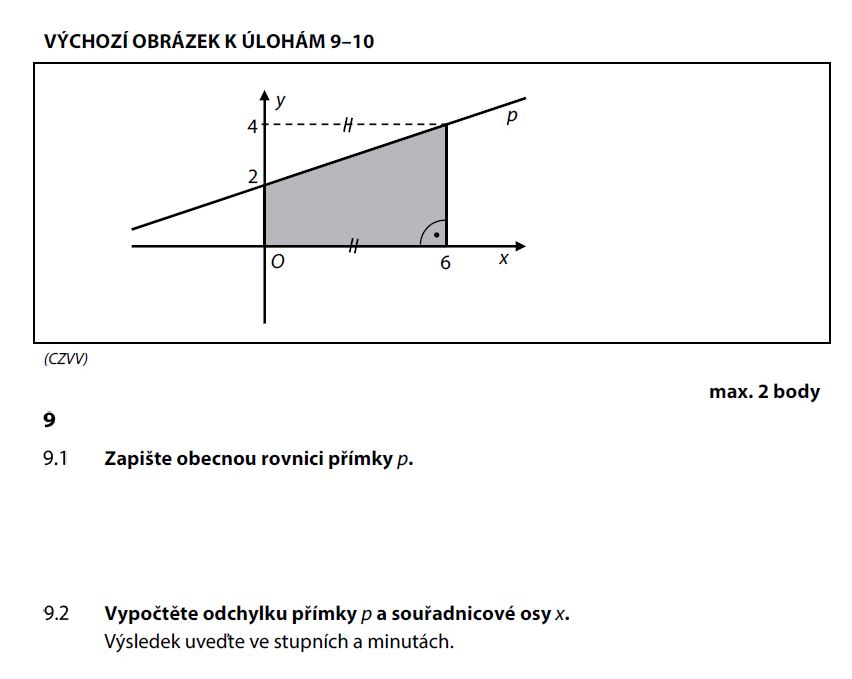
Řešení úlohy 9

Zadání úlohy 10

Řešení úlohy 10

Zadání úlohy 11

Řešení úlohy 11

Zadání úlohy 12

Řešení úlohy 12

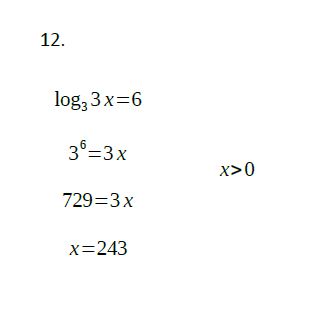
Zadání úlohy 13

Řešení úlohy 13

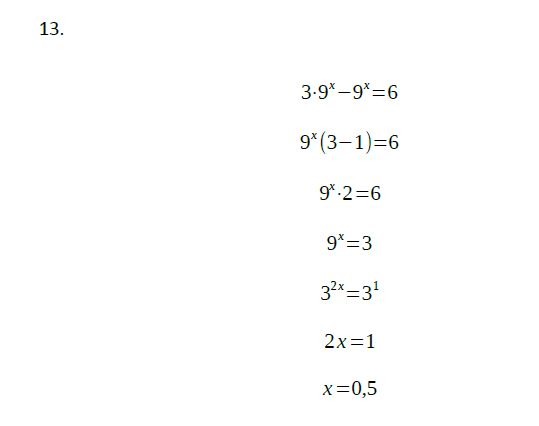
Zadání úlohy 14

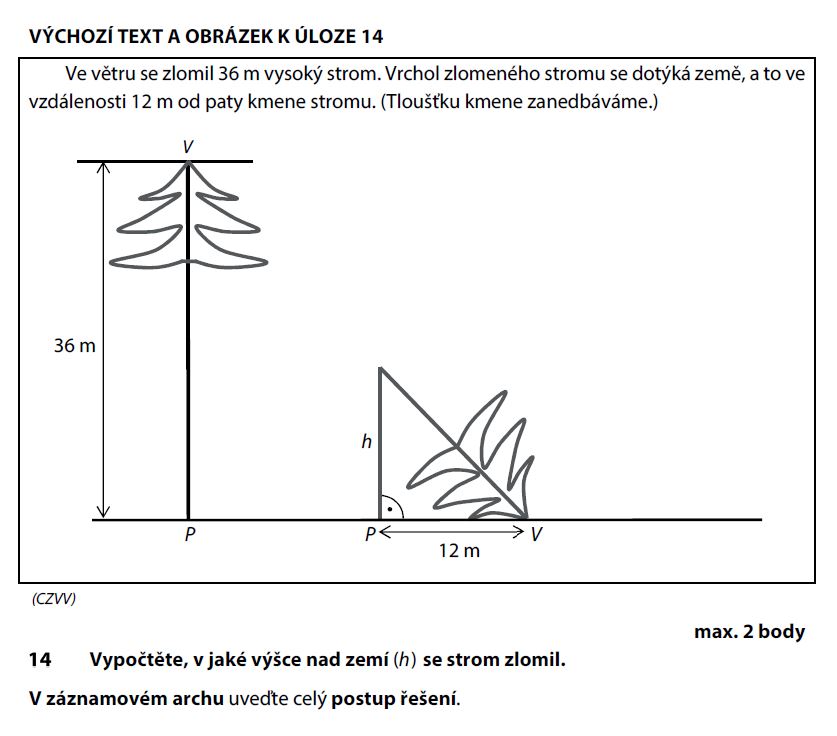
Řešení úlohy 14

Zadání úlohy 15

Řešení úlohy 15

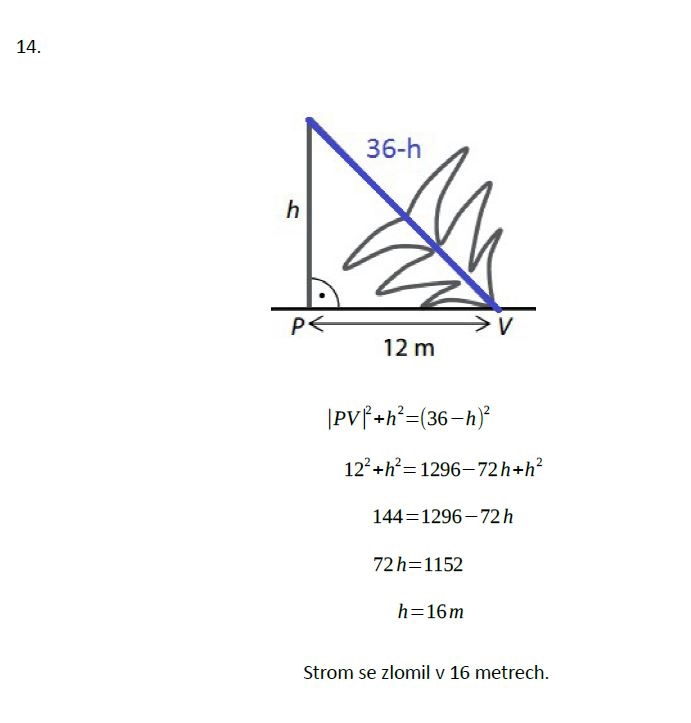
Zadání úlohy 16

Řešení úlohy 16

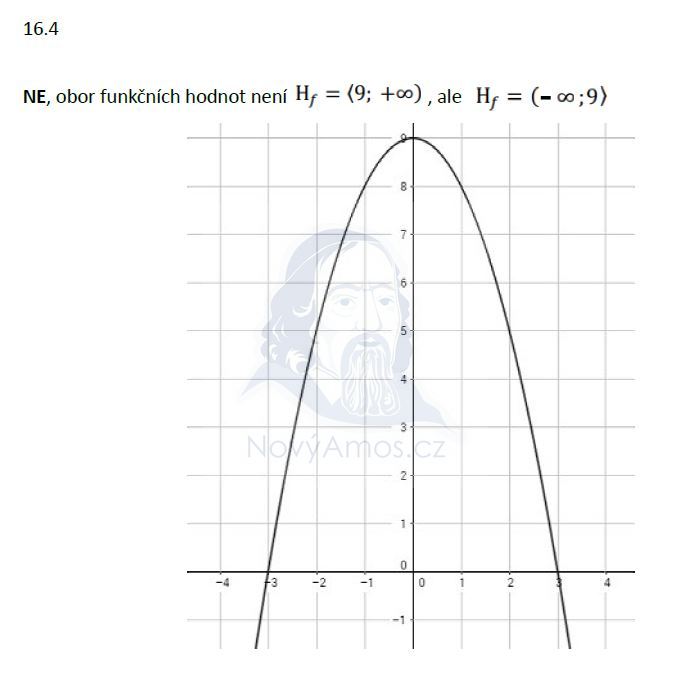
Zadání úlohy 17

Řešení úlohy 17

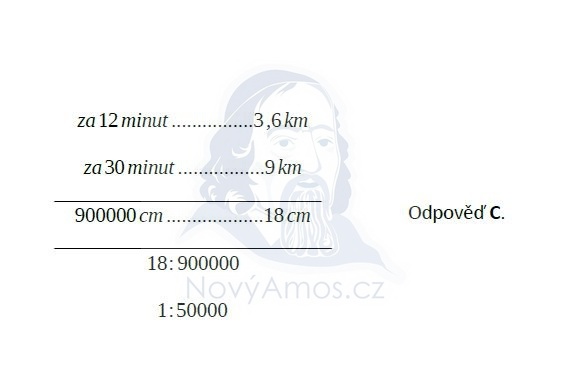
Zadání úlohy 18

Řešení úlohy 18

Zadání úlohy 19

Řešení úlohy 19

Zadání úlohy 20

Řešení úlohy 20

Zadání úlohy 21

Řešení úlohy 21

Zadání úlohy 22

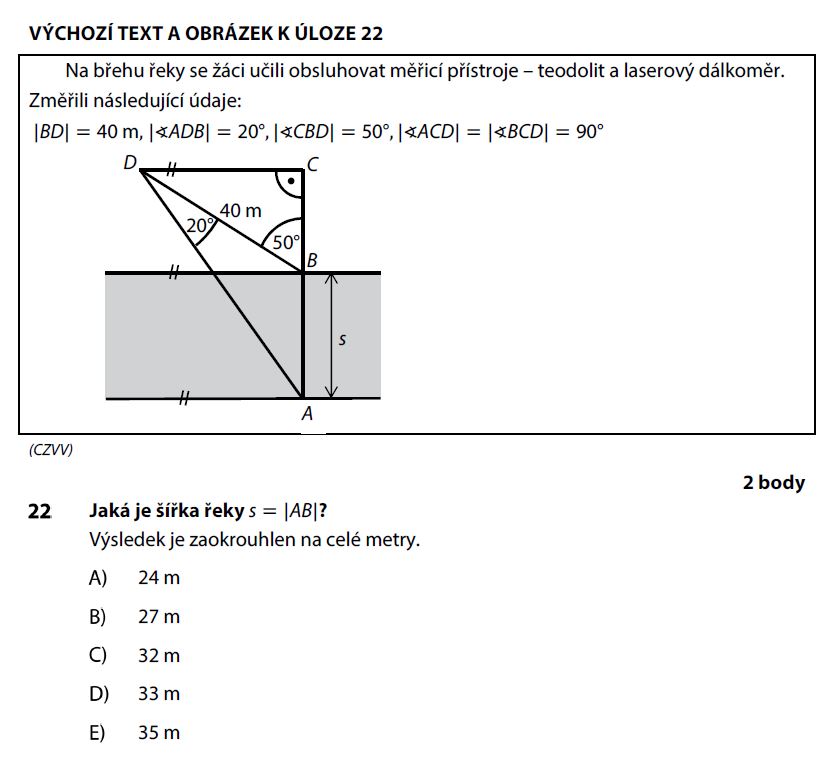
Řešení úlohy 22

Zadání úlohy 23

Řešení úlohy 23

Zadání úlohy 24

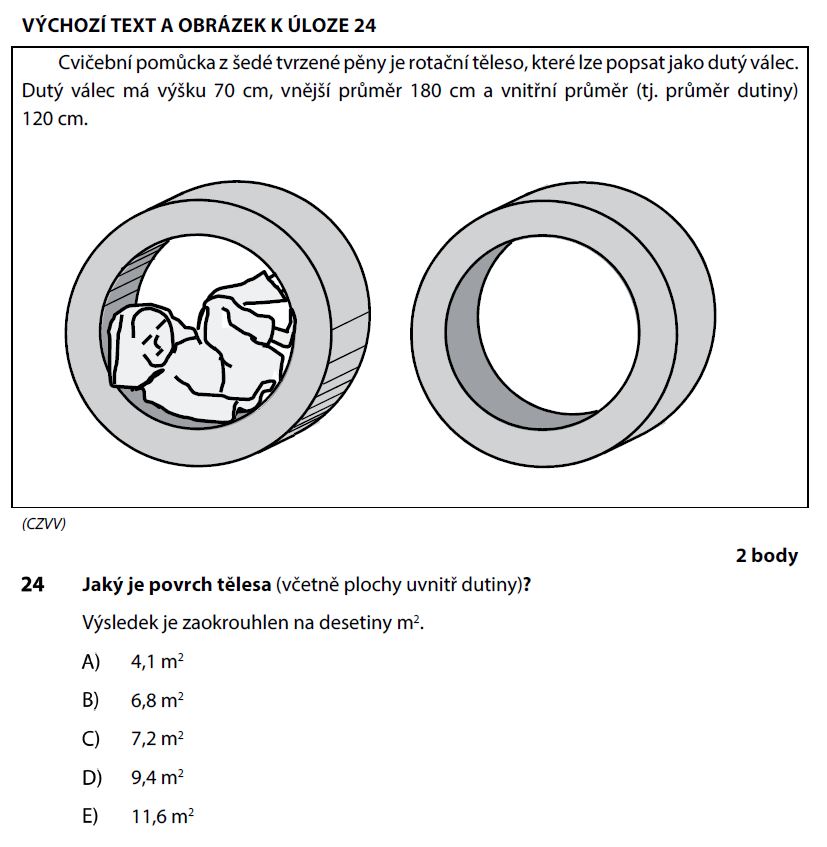
Řešení úlohy 24

Zadání úlohy 25

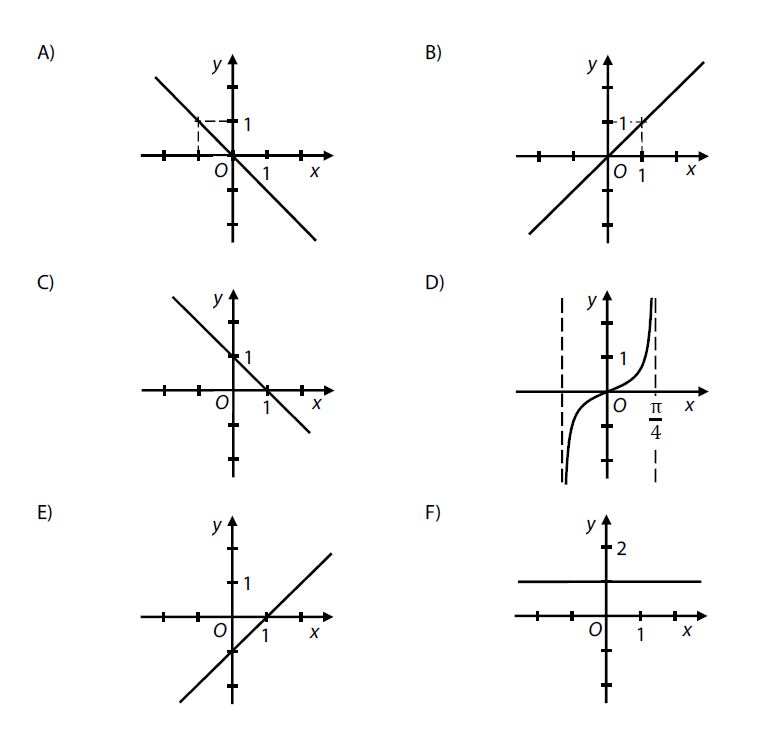
Řešení úlohy 25

Zadání úlohy 26

Řešení úlohy 26

Řešení, zadání a postupy všech matematických maturit

Všechny testy z matematiky předchozích let on-line:

testy 2025 | testy 2024 | testy 2023 | testy 2022 | testy 2021 | testy 2020 | testy 2019 | testy 2018 | testy 2017 | testy 2016 |  testy 2015 | testy 2014 | testy 2013 | testy 2012 | testy 2011 | testy 2010

maturita-cestina-amos-itutoring-footer-content
Řešení

Čtěte také

12 comments

Helena Ošťádalová

Oprava - uvedený výsledek je správný: x - 3y + 6 = 0. 🙂

Odpovědět
Matěj

Ta sedmička je trošku šílená, nemyslíte ? Co takhle uvědomit si jednu zásadní věc. Krychličky jsou skládány na sebe a nesmí horní přesáhnout spodní. To znamená, že při pohledu shora na onu věž, vidíme plný kraj pouze největší krychle tudíž té, která je úplně naspodu a má hranu 6 metrů. Jednoduchým výpočtem se dopočítáváme k součtu celkových nezakrytých vodorovných ploch 36 metrů čtverečních.

Odpovědět
Michal

Není mi jasné z jakého důvodu je třeba u úlohy číslo 4 určovat podmínky. Už ze slovního zadání plyne, že v bodech -5 a 5 není výraz definován.

Odpovědět
Ondřej

...tak ještě jednou... u příkladu 8.2 má být S = A + 1/2 × AC = [-1,1] + (3,2) = [2,3]

ale nic si z toho nedělejte - každý dělá chyby :* (sice ne několikrát po sobě, ale i to se může stát)

Ondra

Odpovědět
Jan

Dobrý den, dáváte v příkladu 4. za špatné řešení aspoň body za stanovení podmínek platnosti? Děkuji

Odpovědět
Kateřina

Jen se chci zeptat, když jste nenapsali ze chcete podmínky u 4 a 5. Je to považováno jako za chybu když je tam nemám ?

Odpovědět
blanka

Děkuji za pěknou a rychlou práci!

Odpovědět
Jan Šmejkal

K úloze 20:
Myslím, že je možné i jiné řešení bez nutnosti počítat "n nad k".
Pravděpodobnost při prvním výběru: 16/25
Pravděpodobnost při druhém výběru: 15/24
Výsledná pravděpodobnost součin: 16/25 * 15/24 = 2/5
Přátele matematiky zdraví Honza

Odpovědět
Maturant

Dobrý den, měla být v záznamovém archu u první úlohy a logaritmu i podmínka?

Odpovědět
Jakub

Dobrý den, měl bych prosím dotaz na úlohu č.15 na mince. Jelikož mi nešli sestavit rovnice, tak jsem na úlohu přišel jinak a postup jak jsem na to přišel jsem jím tam napsal. Myslíte, že dostanu alespoň 1 bod ze 3?

Dále bych se chtěl zeptat jestli úloh č.5 a č.12 musely být podmínky?když se na ně neptají v zadaní.

Děkuji moc za odpověď.

Odpovědět
Viktor Hahn

Řešení úlohy 7:
Očíslujme si krychle od největší po nejmenší 1, 2, ... , 51 a obsah jedné strany těchto krychlí S1, S2, ..., S51. Potom obsah nezakryté vodorovné strany i-té krychle je S(i)-S(i+1).
Celková plocha nezakrytých vodorovných ploch je potom:
(S1 - S2) + (S2 - S3) + ... + (S50 - S51) + S51 = S1 = 6*6 (mimochodem ve výsledku vám chybí druhá mocnina)

Zjednodušeně řečeno, stačí si představit pohled na věž shora. Protože žádná krychle nepřečnívá, to co přidává horní stranou, to samé ubírá překryvem dolní stranou.

Vaše řešení úlohy č.7 je typické středoškolské "postupuj podle návodu v kuchařce". Místo aby se studenti učili o problému uvažovat, biflují se vzorečky a když něco přesně nepasuje na naučený postup, jsou v koncích.

Odpovědět
Jiří Jahoda

Úlohu 7 lze řešit i rychleji, pokud si uvědomíme, že při pohledu shora vidíme všechny nezakryté vodorovné plochy, a ty při tomto pohledu tvoří celý čtverec 6x6m.

Odpovědět

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna. Vyžadované informace jsou označeny *